피마 인디언 당뇨병 데이터셋
피마 인디언의 당뇨병 데이터셋을 이용하여 당뇨병과 상관이 있는 지표를 알아보자.
코드와 그래프
'''
피마 인디언 대상 당뇨병 여부 측정 데이터셋
1) 피마 인디언 데이터
- 샘플 수 : 768개
- 속성 (8개)
- pregnant (과거 임신 횟수)
- plasma (공복 혈당 농도)
- pressure (혈압)
- thickness (심두근 피부 주름 두께)
- insulin (혈청 인슐린)
- bmi (체질량 지수)
- pedigree (당뇨병 가족력)
- age
- 독립 변수
- diabetes (당뇨 1 , 정상 0)
'''
import os
import pandas
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# INFO, WARNING, and ERROR messages are not printed
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
#피마 인디언 당뇨병 데이터셋 불러오기
df = pd.read_csv('./data/pima-indians-diabetes3.csv')
# 첫 10줄 보기
print(df.head(10))
# 정상과 당뇨병 환자가 각각 몇 명인지 확인 (500 : 268)
print(df['diabetes'].value_counts())
# 각 정보별 특징 출력
print(df.describe())
# 각 항목 상관관계 확인
print(df.corr())
# 그래프로 표현
colormap = plt.cm.gist_heat # 그래프 색상 구성
plt.figure(figsize=(12, 12)) # 그래프 크기 정하기
sns.heatmap(df.corr(), linewidths=0.1, vmax=0.5, cmap=colormap, linecolor='white', annot=True)
plt.title('Correlation Heatmap')
plt.show()
sns.heatmap(df.corr(), linewidths=0.1, vmax=0.5, cmap=colormap, linecolor='white', annot=True)위 코드만 따로 해석해 보면
1. df.corr(): DataFrame의 각 열(변수)들 간의 상관관계를 계산한다.
2. sns.heatmap(...): seaborn 라이브러리의 히트맵 함수를 호출한다. 상관계수를 시각화하여 히트맵을 생성한다.
3. linewidths=0.1: 히트맵 내부 셀 사이의 선의 너비를 설정
4. vmax=0.5: 히트맵의 색상 척도(scale)에서 최대 값을 설정. 상관계수가 0.5를 넘는 값은 동일한 색으로 표시함.
5. cmap=colormap: 히트맵의 색상 맵을 설정
6. linecolor='white': 히트맵의 셀 경계선 색상을 흰색으로 설정
7. annot=True: 히트맵의 각 셀에 상관계수 값을 주석으로 표시.
따라서, 주어진 코드는 DataFrame의 변수들 간의 상관관계를 시각적으로 보여주는 히트맵을 생성한다. 상관계수가 0.5를 넘는 값은 짙은 색으로 표시되며, 각 셀에는 상관계수 값이 주석으로 표시된다. 히트맵은 변수들 간의 상관관계를 파악하는 데 도움을 줄 수 있다.
히트맵(heatmap)으로 표현하기

plasma(공복혈당농도)와 당뇨병 사이 상관관계가 있어 보인다.
실제로 공복혈당농도는 당뇨병 진단의 기준이 되기도 한다.
정상적인 대사 과정에서, 음식물 섭취 후 포도당은 소화 과정을 거쳐 혈액으로 흡수되고, 인슐린이라는 호르몬이 혈당을 조절하여 적절한 수준을 유지합니다. 그러나 당뇨병 환자는 인슐린의 분비 부족 또는 인슐린 저항으로 인해 공복혈당농도가 정상 범위를 벗어날 수 있습니다.
일반적으로, 공복혈당농도가 계속해서 상승하면서 당뇨병이 진행될 가능성이 높아집니다. 혈당 조절 기능이 손상되면 신체의 다양한 부분에 부작용이 발생할 수 있으며, 만약 이러한 상황이 지속된다면 당뇨병이 발생할 수 있습니다.
그래프로 표현하기
'''
피마 인디언 대상 당뇨병 여부 측정 데이터셋
1) 피마 인디언 데이터
- 샘플 수 : 768개
- 속성 (8개)
- pregnant (과거 임신 횟수)
- plasma (공복 혈당 농도)
- pressure (혈압)
- thickness (심두근 피부 주름 두께)
- insulin (혈청 인슐린)
- bmi (체질량 지수)
- pedigree (당뇨병 가족력)
- age
- 독립 변수
- diabetes (당뇨 1 , 정상 0)
'''
import os
import pandas
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# INFO, WARNING, and ERROR messages are not printed
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
#피마 인디언 당뇨병 데이터셋 불러오기
df = pd.read_csv('./data/pima-indians-diabetes3.csv')
# 첫 10줄 보기
print(df.head(10))
# 정상과 당뇨병 환자가 각각 몇 명인지 확인 (500 : 268)
print(df['diabetes'].value_counts())
# 각 정보별 특징 출력
print(df.describe())
# 각 항목 상관관계 확인
print(df.corr())
# 그래프로 표현
'''
his() 함수 안에
x축 지정(컬럼)
- diabetes
- plasma
bins : x축을 몇개의 막대로 쪼갤지 정함
'''
colormap = plt.cm.gist_heat # 그래프 색상 구성
plt.figure(figsize=(12, 12)) # 그래프 크기 정하기
plt.hist(x=[df.plasma[df.diabetes == 0], df.plasma[df.diabetes == 1]],
bins=30, histtype='barstacked', label=['normal', 'diabetes'])
plt.legend()
plt.show()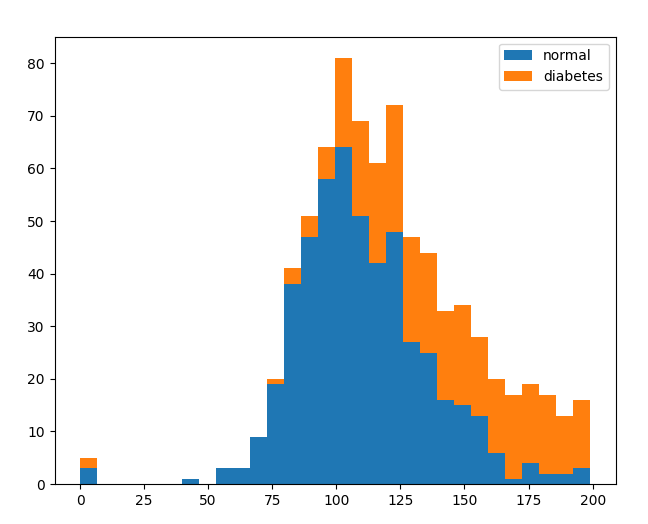
공복혈당과 당뇨병은 밀접하게 관련이 있다.
bmi도 상관이 다른 지표에 비해 높은 것을 볼 수 있다.
# bmi 기준으로 비교해보자
'''
bmi 높아질 경우 당뇨병에 걸릴 확률이 높아지는 것 같아
'''
plt.hist(x=[df.bmi[df.diabetes == 0], df.bmi[df.diabetes == 1]],
bins=30, histtype='barstacked', label=['normal', 'diabetes'])
plt.legend()
plt.show()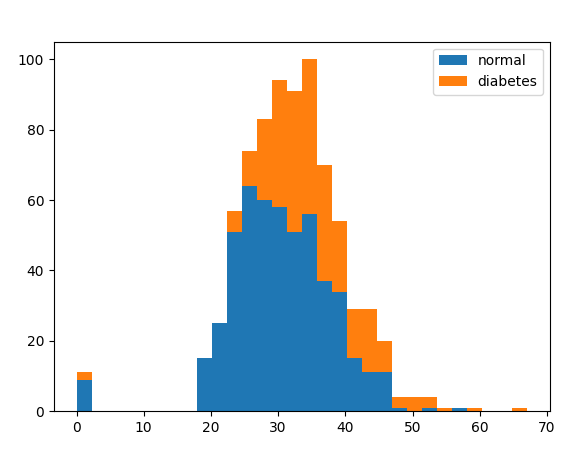
결론은 공복혈당, BMI가 당뇨병 발병과 연관이 있다는 것이다.
단 음식 줄이고 운동하고 살 빼면 어느 정도 해결이 될 것 같다.
학습된 결과
'''
피마 인디언 대상 당뇨병 여부 측정 데이터셋
1) 피마 인디언 데이터
- 샘플 수 : 768개
- 속성 (8개)
- pregnant (과거 임신 횟수)
- plasma (공복 혈당 농도)
- pressure (혈압)
- thickness (심두근 피부 주름 두께)
- insulin (혈청 인슐린)
- bmi (체질량 지수)
- pedigree (당뇨병 가족력)
- age
- 독립 변수
- diabetes (당뇨 1 , 정상 0)
'''
import os
import pandas
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# INFO, WARNING, and ERROR messages are not printed
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
#피마 인디언 당뇨병 데이터셋 불러오기
df = pd.read_csv('./data/pima-indians-diabetes3.csv')
# 첫 10줄 보기
print(df.head(10))
# 정상과 당뇨병 환자가 각각 몇 명인지 확인 (500 : 268)
print(df['diabetes'].value_counts())
# 각 정보별 특징 출력
print(df.describe())
# 각 항목 상관관계 확인
print(df.corr())
# 그래프로 표현
'''
his() 함수 안에
x축 지정(컬럼)
- diabetes
- plasma
bins : x축을 몇개의 막대로 쪼갤지 정함
'''
colormap = plt.cm.gist_heat # 그래프 색상 구성
plt.figure(figsize=(12, 12)) # 그래프 크기 정하기
plt.hist(x=[df.plasma[df.diabetes == 0], df.plasma[df.diabetes == 1]],
bins=30, histtype='barstacked', label=['normal', 'diabetes'])
plt.legend()
plt.show()
# bmi 기준으로 비교해보자
'''
bmi 높아질 경우 당뇨병에 걸릴 확률이 높아지는 것 같아
'''
plt.hist(x=[df.bmi[df.diabetes == 0], df.bmi[df.diabetes == 1]],
bins=30, histtype='barstacked', label=['normal', 'diabetes'])
plt.legend()
plt.show()
######################################################################
# 독립변수를 X로 지정
X = df.iloc[:, 0:8]
# 종속변수(당뇨병 유무 확인)를 y로 지정
y = df.iloc[:, 8]
# 모델 구조 설정
model = Sequential()
model.add(Dense(12, input_dim=8, activation='relu', name='Dense_1'))
model.add(Dense(8, activation='relu', name='Dense_2'))
model.add(Dense(1, activation='sigmoid', name='Dense_3'))
model.summary()
# 모델을 컴파일
model.compile(loss='binary_crossentropy', optimizer='adam',
metrics=['accuracy'])
#모델 학습(실행)
model.fit(X, y, epochs=100, batch_size=5)Epoch 1/100
154/154 [==============================] - 1s 925us/step - loss: 2.5410 - accuracy: 0.4284
Epoch 2/100
154/154 [==============================] - 0s 906us/step - loss: 1.1578 - accuracy: 0.5312
Epoch 3/100
154/154 [==============================] - 0s 932us/step - loss: 0.8425 - accuracy: 0.6224
Epoch 4/100
154/154 [==============================] - 0s 880us/step - loss: 0.7572 - accuracy: 0.6380
Epoch 5/100
154/154 [==============================] - 0s 841us/step - loss: 0.7121 - accuracy: 0.6523
Epoch 6/100
154/154 [==============================] - 0s 900us/step - loss: 0.6844 - accuracy: 0.6536
Epoch 7/100
154/154 [==============================] - 0s 900us/step - loss: 0.6575 - accuracy: 0.6458
Epoch 8/100
154/154 [==============================] - 0s 828us/step - loss: 0.6397 - accuracy: 0.6680
Epoch 9/100
154/154 [==============================] - 0s 880us/step - loss: 0.6669 - accuracy: 0.6654
Epoch 10/100
154/154 [==============================] - 0s 821us/step - loss: 0.6284 - accuracy: 0.6654
Epoch 11/100
154/154 [==============================] - 0s 847us/step - loss: 0.6191 - accuracy: 0.6849
Epoch 12/100
154/154 [==============================] - 0s 880us/step - loss: 0.6260 - accuracy: 0.6680
Epoch 13/100
154/154 [==============================] - 0s 815us/step - loss: 0.6258 - accuracy: 0.6719
Epoch 14/100
154/154 [==============================] - 0s 860us/step - loss: 0.6036 - accuracy: 0.6953
Epoch 15/100
154/154 [==============================] - 0s 795us/step - loss: 0.6101 - accuracy: 0.6810
Epoch 16/100
154/154 [==============================] - 0s 834us/step - loss: 0.5992 - accuracy: 0.6810
Epoch 17/100
154/154 [==============================] - 0s 847us/step - loss: 0.5995 - accuracy: 0.6927
Epoch 18/100
154/154 [==============================] - 0s 860us/step - loss: 0.6014 - accuracy: 0.6953
Epoch 19/100
154/154 [==============================] - 0s 893us/step - loss: 0.5922 - accuracy: 0.6927
Epoch 20/100
154/154 [==============================] - 0s 782us/step - loss: 0.5892 - accuracy: 0.6901
Epoch 21/100
154/154 [==============================] - 0s 1ms/step - loss: 0.5835 - accuracy: 0.6979
Epoch 22/100
154/154 [==============================] - 0s 815us/step - loss: 0.5757 - accuracy: 0.7174
Epoch 23/100
154/154 [==============================] - 0s 900us/step - loss: 0.5757 - accuracy: 0.7174
Epoch 24/100
154/154 [==============================] - 0s 815us/step - loss: 0.5801 - accuracy: 0.7083
Epoch 25/100
154/154 [==============================] - 0s 1ms/step - loss: 0.5791 - accuracy: 0.7148
Epoch 26/100
154/154 [==============================] - 0s 847us/step - loss: 0.5693 - accuracy: 0.7409
Epoch 27/100
154/154 [==============================] - 0s 808us/step - loss: 0.5746 - accuracy: 0.7227
Epoch 28/100
154/154 [==============================] - 0s 893us/step - loss: 0.5566 - accuracy: 0.7422
Epoch 29/100
154/154 [==============================] - 0s 854us/step - loss: 0.5751 - accuracy: 0.7044
Epoch 30/100
154/154 [==============================] - 0s 821us/step - loss: 0.5739 - accuracy: 0.7070
Epoch 31/100
154/154 [==============================] - 0s 880us/step - loss: 0.5643 - accuracy: 0.7201
Epoch 32/100
154/154 [==============================] - 0s 821us/step - loss: 0.5630 - accuracy: 0.7188
Epoch 33/100
154/154 [==============================] - 0s 854us/step - loss: 0.5798 - accuracy: 0.7005
Epoch 34/100
154/154 [==============================] - 0s 776us/step - loss: 0.5596 - accuracy: 0.7305
Epoch 35/100
154/154 [==============================] - 0s 880us/step - loss: 0.5723 - accuracy: 0.7018
Epoch 36/100
154/154 [==============================] - 0s 1ms/step - loss: 0.5624 - accuracy: 0.7214
Epoch 37/100
154/154 [==============================] - 0s 795us/step - loss: 0.5523 - accuracy: 0.7344
Epoch 38/100
154/154 [==============================] - 0s 873us/step - loss: 0.5596 - accuracy: 0.7122
Epoch 39/100
154/154 [==============================] - 0s 906us/step - loss: 0.5705 - accuracy: 0.7305
Epoch 40/100
154/154 [==============================] - 0s 926us/step - loss: 0.5485 - accuracy: 0.7357
Epoch 41/100
154/154 [==============================] - 0s 880us/step - loss: 0.5409 - accuracy: 0.7292
Epoch 42/100
154/154 [==============================] - 0s 873us/step - loss: 0.5758 - accuracy: 0.7279
Epoch 43/100
154/154 [==============================] - 0s 847us/step - loss: 0.5632 - accuracy: 0.7135
Epoch 44/100
154/154 [==============================] - 0s 802us/step - loss: 0.5547 - accuracy: 0.7214
Epoch 45/100
154/154 [==============================] - 0s 834us/step - loss: 0.5414 - accuracy: 0.7279
Epoch 46/100
154/154 [==============================] - 0s 834us/step - loss: 0.5541 - accuracy: 0.7331
Epoch 47/100
154/154 [==============================] - 0s 828us/step - loss: 0.5372 - accuracy: 0.7383
Epoch 48/100
154/154 [==============================] - 0s 952us/step - loss: 0.5617 - accuracy: 0.7240
Epoch 49/100
154/154 [==============================] - 0s 860us/step - loss: 0.5504 - accuracy: 0.7227
Epoch 50/100
154/154 [==============================] - 0s 854us/step - loss: 0.5459 - accuracy: 0.7292
Epoch 51/100
154/154 [==============================] - 0s 900us/step - loss: 0.5808 - accuracy: 0.7201
Epoch 52/100
154/154 [==============================] - 0s 841us/step - loss: 0.5559 - accuracy: 0.7174
Epoch 53/100
154/154 [==============================] - 0s 1ms/step - loss: 0.5367 - accuracy: 0.7513
Epoch 54/100
154/154 [==============================] - 0s 887us/step - loss: 0.5332 - accuracy: 0.7500
Epoch 55/100
154/154 [==============================] - 0s 808us/step - loss: 0.5794 - accuracy: 0.7188
Epoch 56/100
154/154 [==============================] - 0s 860us/step - loss: 0.5568 - accuracy: 0.7174
Epoch 57/100
154/154 [==============================] - 0s 802us/step - loss: 0.5234 - accuracy: 0.7500
Epoch 58/100
154/154 [==============================] - 0s 847us/step - loss: 0.5230 - accuracy: 0.7526
Epoch 59/100
154/154 [==============================] - 0s 887us/step - loss: 0.5334 - accuracy: 0.7461
Epoch 60/100
154/154 [==============================] - 0s 756us/step - loss: 0.5330 - accuracy: 0.7422
Epoch 61/100
154/154 [==============================] - 0s 815us/step - loss: 0.5347 - accuracy: 0.7383
Epoch 62/100
154/154 [==============================] - 0s 789us/step - loss: 0.5401 - accuracy: 0.7461
Epoch 63/100
154/154 [==============================] - 0s 860us/step - loss: 0.5377 - accuracy: 0.7331
Epoch 64/100
154/154 [==============================] - 0s 782us/step - loss: 0.5330 - accuracy: 0.7357
Epoch 65/100
154/154 [==============================] - 0s 795us/step - loss: 0.5366 - accuracy: 0.7344
Epoch 66/100
154/154 [==============================] - 0s 808us/step - loss: 0.5311 - accuracy: 0.7370
Epoch 67/100
154/154 [==============================] - 0s 763us/step - loss: 0.5269 - accuracy: 0.7344
Epoch 68/100
154/154 [==============================] - 0s 815us/step - loss: 0.5393 - accuracy: 0.7461
Epoch 69/100
154/154 [==============================] - 0s 763us/step - loss: 0.5230 - accuracy: 0.7448
Epoch 70/100
154/154 [==============================] - 0s 834us/step - loss: 0.5195 - accuracy: 0.7422
Epoch 71/100
154/154 [==============================] - 0s 795us/step - loss: 0.5222 - accuracy: 0.7474
Epoch 72/100
154/154 [==============================] - 0s 1ms/step - loss: 0.5371 - accuracy: 0.7578
Epoch 73/100
154/154 [==============================] - 0s 926us/step - loss: 0.5191 - accuracy: 0.7578
Epoch 74/100
154/154 [==============================] - 0s 919us/step - loss: 0.5435 - accuracy: 0.7253
Epoch 75/100
154/154 [==============================] - 0s 965us/step - loss: 0.5310 - accuracy: 0.7422
Epoch 76/100
154/154 [==============================] - 0s 919us/step - loss: 0.5104 - accuracy: 0.7617
Epoch 77/100
154/154 [==============================] - 0s 828us/step - loss: 0.5165 - accuracy: 0.7487
Epoch 78/100
154/154 [==============================] - 0s 893us/step - loss: 0.5135 - accuracy: 0.7513
Epoch 79/100
154/154 [==============================] - 0s 841us/step - loss: 0.5097 - accuracy: 0.7669
Epoch 80/100
154/154 [==============================] - 0s 952us/step - loss: 0.5238 - accuracy: 0.7448
Epoch 81/100
154/154 [==============================] - 0s 815us/step - loss: 0.5297 - accuracy: 0.7565
Epoch 82/100
154/154 [==============================] - 0s 828us/step - loss: 0.5269 - accuracy: 0.7474
Epoch 83/100
154/154 [==============================] - 0s 873us/step - loss: 0.5217 - accuracy: 0.7435
Epoch 84/100
154/154 [==============================] - 0s 815us/step - loss: 0.5125 - accuracy: 0.7630
Epoch 85/100
154/154 [==============================] - 0s 893us/step - loss: 0.5184 - accuracy: 0.7552
Epoch 86/100
154/154 [==============================] - 0s 802us/step - loss: 0.5225 - accuracy: 0.7422
Epoch 87/100
154/154 [==============================] - 0s 834us/step - loss: 0.5250 - accuracy: 0.7526
Epoch 88/100
154/154 [==============================] - 0s 926us/step - loss: 0.5099 - accuracy: 0.7682
Epoch 89/100
154/154 [==============================] - 0s 841us/step - loss: 0.5016 - accuracy: 0.7370
Epoch 90/100
154/154 [==============================] - 0s 965us/step - loss: 0.5063 - accuracy: 0.7643
Epoch 91/100
154/154 [==============================] - 0s 900us/step - loss: 0.5068 - accuracy: 0.7435
Epoch 92/100
154/154 [==============================] - 0s 841us/step - loss: 0.5050 - accuracy: 0.7578
Epoch 93/100
154/154 [==============================] - 0s 919us/step - loss: 0.5030 - accuracy: 0.7565
Epoch 94/100
154/154 [==============================] - 0s 821us/step - loss: 0.5087 - accuracy: 0.7552
Epoch 95/100
154/154 [==============================] - 0s 841us/step - loss: 0.5083 - accuracy: 0.7578
Epoch 96/100
154/154 [==============================] - 0s 913us/step - loss: 0.5143 - accuracy: 0.7500
Epoch 97/100
154/154 [==============================] - 0s 808us/step - loss: 0.5037 - accuracy: 0.7656
Epoch 98/100
154/154 [==============================] - 0s 900us/step - loss: 0.5050 - accuracy: 0.7565
Epoch 99/100
154/154 [==============================] - 0s 834us/step - loss: 0.5102 - accuracy: 0.7552
Epoch 100/100
154/154 [==============================] - 0s 860us/step - loss: 0.5130 - accuracy: 0.7578
위 모델을 이용해서 개인의 정보를 입력으로 받고, 그 개인이 당뇨병에 걸릴 가능성을 예측할 수 있다.
'Python' 카테고리의 다른 글
| [파이썬] 기억력 테스트 게임 만들기. Random 모듈 사용 (1) | 2023.07.08 |
|---|---|
| 텐서플로(tensorflow)를 이용한 인공신경망 구현 (1) | 2023.06.27 |
| [파이썬] figure창 자동으로 닫는 방법 - plt.pause(), plt.close() (1) | 2023.06.21 |
| [Python] 파이썬 예외 처리 (try ~ except). java와 다른 점? (2) | 2023.06.20 |
| 파이썬 pandas.Series는 무엇인가? (1) | 2023.05.31 |

